Here to keep the car on the track and prevent in from skiding, frictional force is required. Since the car is moving on a curve this frictional force is provided in the form of centripetal force.
Centripetal force is given as,
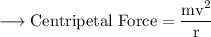
Since the curve is unbanked, frictional force is given as,
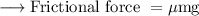
where ,
- m is the mass of the car.
- v is the velocity of the car.
- r is the radius of the curve.
- μ is the coefficient of static friction.
- g is acceleration due to gravity.
So we have;
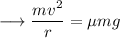
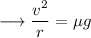
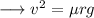
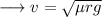
This velocity is the maximum velocity beyond which the car will begin to skid. On substituting the respective values, we have;
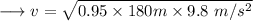
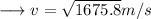
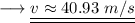
Hence the car begins to skid approximately at a velocity of 41m/s.