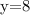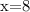Question

Using the modeled equation in the box, create an algebraic equation and solve for X.

Answer 1

The solution to the system of equations is
`\(x = 8\)` and
`\(y = 8\)`. The alternative method using elimination confirms the same result. The system is consistent and has a unique solution:
`\((8, 8)\)`.

Let’s solve the system of equations:

`$$y=-x+t-1$$`

`$$x=8$$`

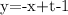
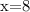
We can solve the system of equations by substituting the second equation into the first equation.

Steps to solve:

1. Rearrange terms in standard form:

`$$y+x-t=-1$$`

`$$x=8$$`

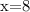
2. Substitute in the equations:

`$$y-t=-9$$`

`$$x=8$$`

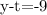
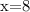
3. Solve for y:

`$$y=t-9$$`

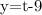
4. Substitute the value of y into the second equation:

`$$t-9=8$$`

`$$t=17$$`

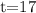
Answer:

`$$y=t-9$$`

`$$y=17-9$$`

`$$y=8$$`

`$$x=8$$`

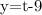
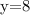
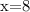
Alternatively, we can use elimination method:

1. Multiply the top equation by -1:

`$$-y-x+t=1$$`

`$$x=8$$`

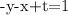
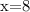
2. Add the top and bottom equations:

`$$t=9$$`

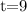
3. Substitute the value of t into the top equation:

`$$y=-x+9-1$$`

`$$y=-x+8$$`

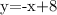
4. Substitute the value of x into the equation:

`$$y=-(8)+8$$`

`$$y=0$$`

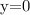
Therefore, the solution is:

`$$y=8$$`

`$$x=8$$`