Question

Explain how you can use your answer to Part A to predict, within the context of the situation, where Kelly is at time t minutes.​

Answer 1

(a) **Part A:**

The value of y when x=1 is 200 feet. At time 1 minute, Kelly has walked a distance of 200 feet.

(b) **Part B:**

Using the constant rate of change, Kelly's distance at any time t can be predicted with the formula y=200t, where t is the time in minutes.

(a) **Part A:

According to the information provided, at time 1 minute (when x=1), Kelly reaches a distance of 200 feet. Therefore, the value of y when x=1 is 200 feet.

(b) **Part B:

The scenario describes a situation where Kelly is walking a uniform distance in uniform time. The relationship between time (x) and distance (y) is linear, and it appears to have a constant rate of change. In this case, the rate of change is
`\( \frac{\text{change in distance}}{\text{change in time}} \).`

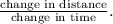
From the given information:

- At
`\( t = 1 \)` minute,
`\( y = 200 \)` feet.

- At
`\( t = 2 \)` minutes,
`\( y = 400 \)` feet (an increase of 200 feet from the previous minute).

- At
`\( t = 3 \)` minutes,
`\( y = 600 \)` feet (an increase of 200 feet from the previous minute).

Each minute, the distance traveled increases by 200 feet. Therefore, you can predict where Kelly is at any time
`\( t \)` by using the formula:

`\[ y = 200t \]`

So, if you want to find where Kelly is at
`\( t = 4 \)` minutes, you can substitute
`\( t = 4 \)` into the formula:

`\[ y = 200 * 4 = 800 \]`

This tells you that at
`\( t = 4 \)` minutes, Kelly is 800 feet away from the starting point. This linear relationship allows you to predict Kelly's distance at any given time based on the constant rate of change.

The question probable maybe:
19 The graph below relates y, the distance Kelly walked, to x, the amount of time that Kelly walked.
(a) B Time (minutes) Part A What is the value of y when x=1 ?
Part B Explain how you can use your answer to Part A to predict, within the context of the situation, where Kelly is at time t minutes.