Question

Consider the following figure.

(Note that the figure is not drawn to scale.)
J
81°
I
55°
L
16°
K
Order the side lengths IJ, JL, IK, IL, and LK from
least to greatest.

Answer 1

IJ < JL < IL < LK < IK

Explanation:

To be able to order the side lengths of figure IJKL, we first need to calculate the missing angles.

Given that the interior angles of a triangle sum to 180°, the measure of angle ILJ in triangle IJL can be found by subtracting its two other interior angles from 180°:

m∠ILJ = 180° - m∠IJL - m∠JIL

m∠ILJ = 180° - 55° - 81°

m∠ILJ = 44°

Given that angles on a straight line sum to 180°, the measure of angle ILK can be found by subtracting m∠ILJ from 180°:

m∠ILK = 180° - m∠ILJ

m∠ILK = 180° - 44°

m∠ILK = 136°

Given that the interior angles of a triangle sum to 180°, the measure of angle KIL in triangle ILK can be found by subtracting its other two interior angles from 180°:

m∠KIL = 180° - m∠ILK - m∠LKI

m∠KIL = 180° - 136° - 16°

m∠KIL = 28°

According to the Triangle Inequality Theorem:

• The smallest angle is opposite the shortest side.
• The medium-sized angle is opposite the medium-sized side.
• The largest angle is opposite the longest side.

In triangle IJL, the smallest angle is opposite side IJ, and the largest angle is opposite side IL, so the order of the side lengths is:

• IJ < JL < IL

In triangle IKL, the smallest angle is opposite side IL, and the largest angle is opposite side IK, so the order of the side lengths is:

• IL < LK < IK

Therefore, the side lengths IJ, JL, IK, IL and LK can be ordered from least to greatest as follows:

`\Large\boxed{\boxed{IJ < JL < IL < LK < IK}}`

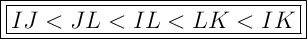
Note: The attached triangle is drawn to scale, confirming the order of the side lengths.