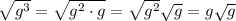Question

Simplify the expression √/45g³h6 by answering each question and checking your answer before moving to the next step.

Step 1: Rewrite √45 as the product of two square root factors, one of which is a perfect square. Then simplify the expression.
Use the keypad to enter the answers in the boxes.
√45==
C
Simplify the expression √45g³h6 by answering each question and checking your answer before moving to the next step.
Step 2: Rewrite √g using square roots of perfect square factors. (Hint: you will have two radicals in your first answer.) Then simp
expression.
Use the keypad to enter the answers in the boxes.
√³--0
Chec

Need done ASAP!

Answer 1

`\textsf{Step 1:}\quad √(45)=\boxed{√(9 \cdot 5)}=\boxed{3√(5)}`

`\textsf{Step 1:}\quad √(g^3)=\boxed{√(g^2 \cdot g)}=\boxed{g√(g)}`

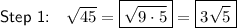
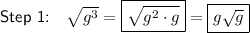
Explanation:

Given expression:

`√(45g^3h^6)`

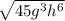
Step 1

To rewrite
`√(45)` as the product of two square root factors, one of which is a perfect square, we first need to find the factors of 45.

The factors of 45 are 1, 3, 5, 9, 15 and 45.

The only factor that is a perfect square is 9, since it can be expressed as 3². Therefore, we can rewrite 45 as the product of 9 and 5.

`√(45)=√(9 \cdot 5)=√(3^2 \cdot 5)=√(3^2)√(5)=3√(5)`

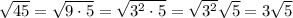
Step 2

To rewrite
`√(g^3)` using square roots of perfect square factors, we first need to apply the product law of exponents and rewrite g³ as:

`g^3=g^(2+1)=g^2 \cdot g^1=g^2 \cdot g`

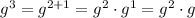
Therefore:

`√(g^3)=√(g^2 \cdot g)=√(g^2)√(g)=g√(g)`