Question

Cindy Jo's Hair Salon is concerned about its rising costs of supplies, energy, and labor, so it is considering investing in better equipment, which hopefully will reduce the time required to perform most hairstyles as well as result in better perceived quality by its customers. It predicts that the added investment will increase output levels as well as reduce energy costs, since some of the new equipment (hair dryers) use less electricity.

Inputs and Outputs Current (this year) Expected (next year)
Hairstyles per week 280 350
Labor costs per week $950 $990
Energy costs per week $400 $370
Material costs per week $350 $385
Capital investment $0 $11,000
Using the given information, determine the current and expected single-factor and total productivity measures. Do not round intermediate calculations. Round your answers to three decimal places.
Productivity Current (this year) Expected (next year)
Labor haircuts/dollar haircuts/dollar
Energy haircuts/dollar haircuts/dollar
Material haircuts/dollar haircuts/dollar
Total haircuts/dollar haircuts/dollar
What is the percentage change in total productivity? Do not round intermediate calculations. Round your answer to two decimal places.
%

Answer 1

The percentage change in total productivity is approximately
`\( 3.70\% \)`.

How did we get the value?

To calculate the productivity measures, you can use the following formulas:

1. Single-Factor Productivity (SFP):

- Labor Productivity: Hairstyles per week / Labor costs per week

- Energy Productivity: Hairstyles per week / Energy costs per week

- Material Productivity: Hairstyles per week / Material costs per week

2. Total Productivity (TP):

- Total Productivity: Hairstyles per week / (Labor costs per week + Energy costs per week + Material costs per week)

To calculate the percentage change in total productivity:

`\[ \text{Percentage Change} = \left( \frac{\text{Expected TP} - \text{Current TP}}{\text{Current TP}} \right) * 100 \]`

Plug in the values and calculate.

Current (this year):

1. Labor Productivity:
`\( (280)/(950) \approx 0.294 \) haircuts/dollar`

2. Energy Productivity:
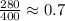`\( (280)/(400) \approx 0.7 \)` haircuts/dollar

3. Material Productivity:
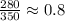`\( (280)/(350) \approx 0.8 \)` haircuts/dollar

4. Total Productivity:
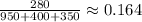`\( (280)/(950 + 400 + 350) \approx 0.164 \)`haircuts/dollar

Expected (next year):

1. Labor Productivity:
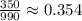`\( (350)/(990) \approx 0.354 \)` haircuts/dollar

2. Energy Productivity:
`\( (350)/(370) \approx 0.946 \)` haircuts/dollar

3. Material Productivity:
`\( (350)/(385) \approx 0.909 \)` haircuts/dollar

4. Total Productivity:
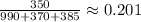`\( (350)/(990 + 370 + 385) \approx 0.201 \)`haircuts/dollar

Now, plug in the values into the percentage change formula:

`\[ \text{Percentage Change}` =
`\left( (0.201 - 0.164)/(0.164) \right) * 100 \approx 3.70\%`

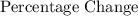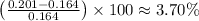
Therefore, the percentage change in total productivity is approximately
`\( 3.70\% \)`.