a. It is shown that
 is greater than
is greater than
 .
.
b. The present value of receiving
 at
at
 years from now is equal to the present value of receiving
years from now is equal to the present value of receiving
 at
at
 years from now for any value of
years from now for any value of
 .
.
How did we arrive at this assertion?
The formula for the present value (PV) of a future amount (FV) compounded annually is given by:
![\[PV = (FV)/((1 + r)^n)\]](https://img.qammunity.org/2024/formulas/medicine/college/d4czm1uin4w95ob56javzrua9cqdb8n877.png)
where:
-
 is the present value,
is the present value,
-
 is the future value,
is the future value,
-
 is the interest rate per period, and
is the interest rate per period, and
-
 is the number of periods.
is the number of periods.
To show that
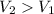
We are given that the present value of receiving
 in 12 years is the same as the present value of receiving
in 12 years is the same as the present value of receiving
 in 4 years.
in 4 years.
![\[ (V_2)/((1 + r)^(12)) = (V_1)/((1 + r)^4) \]](https://img.qammunity.org/2024/formulas/business/college/546tz81vfdvoz5ih39fov7pvr89imj62lf.png)
Cancel out the denominators and rearrange the equation:
![\[ V_2 = V_1 \cdot (1 + r)^(12-4) \]](https://img.qammunity.org/2024/formulas/business/college/z1p8p8ympxwv6fkf5g762mnxunm3hm5p1l.png)
![\[ V_2 = V_1 \cdot (1 + r)^8 \]](https://img.qammunity.org/2024/formulas/business/college/cw89szgigfclp0fca8oxj5zoigjk1cwza7.png)
Since
 (because
(because
 , it follows that
, it follows that
 .
.
(b) Show that the present value of receiving
 ,
,
 years from now, is also equal to the present value of receiving
years from now, is also equal to the present value of receiving
 ,
,
 years from now, for any value of
years from now, for any value of
 .
.
We are asked to show that:
![\[ (V_2)/((1 + r)^(2+k)) = (V_1)/((1 + r)^(t+k)) \]](https://img.qammunity.org/2024/formulas/business/college/aei3evilhrqqokl9rpl8mnscqamxqhndno.png)
Cancel out the denominators and rearrange the equation:
![\[ V_2 = V_1 \cdot \left( ((1 + r)^(t+k))/((1 + r)^(2+k)) \right) \]](https://img.qammunity.org/2024/formulas/business/college/59hfifw276xr61x6i9ghltkqn3htx29rzp.png)
Simplify the expression:
![\[ V_2 = V_1 \cdot (1 + r)^(t-k) \]](https://img.qammunity.org/2024/formulas/business/college/cm8thg2q4lg265mcm0om7v85grxsq1an1l.png)
This shows that the present value of receiving

 years from now is equal to the present value of receiving
years from now is equal to the present value of receiving
 years from now for any value of
years from now for any value of
 .
.
Therefore, the present value of receiving
 at
at
 years from now is equal to the present value of receiving
years from now is equal to the present value of receiving
 at
at
 years from now for any value of
years from now for any value of
 .
.
Complete question:
3. Suppose that the interest rate (r) is such that the present value of receiving $V2 in 12 years from now is the same as the present value of receiving $
 in four years from now, 12>4. Assume that interest is compounded annually.
in four years from now, 12>4. Assume that interest is compounded annually.
(a) Show that V₂ >
 .
.
(b) Show that the present value of receiving $V2, (2+k) years from now is also equal to the present value of receiving $V₁, (t+k) years from now for any value of k. (That is, it is the absolute difference between time periods that matter.)