Question

Dx/(x−1)²(x²+1) = In (x²+1)1/4/√x-1 1 12(x-1) + c.​

Answer 1

To integrate the given expression, we can use partial fractions. Factoring the denominator allows us to rewrite the expression using partial fractions. By comparing numerators, we can find the constants in the partial fraction decomposition. Integrating each term separately gives the final result that is
`$$\ln|x-1|+i\ln|x+i|-i\ln|x-i|+c$$`

The given expression is:

`$$(dx)/((x-1)^2(x^2+1))$$`

To integrate this expression, we can use partial fractions. First, let's factor the denominator:

`$$(dx)/((x-1)^2(x^2+1))$$`

Now, we can write the expression as:

`$$(A)/(x-1)+(Bi)/(x+i)+(Ci)/(x-i)$$`

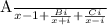
Here, A, B, and C are constants to be determined. We can now find the values of A, B, and C by comparing the numerators:

`$$A(x^2+1)+(x+i)(Ci)+(x-i)(Bi)\;=\;dx$$`

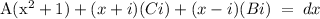
Now, we can integrate each term separately:

`$$\int A(1)/(x-1)dx\;+\;\int B(i)/(x+i)dx\;+\;\int C(-i)/(x-i)dx$$`

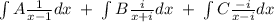
Integrating each term gives:

`$$A\ln|x-1|+Bi\ln|x+i|+Ci\ln|x-i|+c$$`

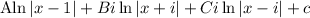
So, the integral of the given expression is:

`$$\ln|x-1|+i\ln|x+i|-i\ln|x-i|+c$$`