The measure of an exterior angle in a regular polygon is calculated by dividing 360° by the number of sides. This concept is key to precision in fields like architecture and design.
The measure of one exterior angle in a regular polygon is determined by the formula:
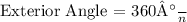
where 'n' is the number of sides in the polygon. This formula is derived from the principle that the sum of all exterior angles in any polygon is always 360°.
For instance, consider a regular heptagon (a polygon with seven sides). Using the formula, the measure of one exterior angle would be approximately 51.4° (360°/7).
This concept is fundamental to understanding the geometric properties of polygons. As the number of sides in a polygon increases, making it more similar to a circle, each exterior angle becomes smaller. Conversely, a polygon with fewer sides will have larger exterior angles.
In practical applications, such as architecture or design, knowing these angles is crucial. It allows for the construction of shapes with precision and accuracy, ensuring that structures are both stable and aesthetically pleasing, while also meeting functional requirements.