Question

Find​ y, ST, and TU.

Answer 1

By analyzing the triangle as a combination of a rectangle and a right triangle, using the Pythagorean theorem, and solving the resulting quadratic equation, we found that y ≈ 15.82, ST ≈ 41.64, and TU ≈ 19.82.

We need to find the lengths of all three sides.

Analyzing the triangle:

Rectangle and right triangle combination: The figure combines a rectangle (VSTU) with a right triangle (SUT). We can use the properties of both shapes to solve for the missing side lengths.

Vertical side: We are given that the vertical side (y) is 2y + 8. However, we need to isolate y to find its actual value.

Solving for y:

Identify a usable equation: We notice that the length TU is also the hypotenuse of the right triangle SUT. Therefore, we can use the Pythagorean theorem:
`TU^2 = SU^2 + ST^2`.

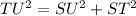Substitute known values: We are given that TU = y + 4 and ST = 2y + 8. Substituting these values, we get:
`(y + 4)^2 = (2y + 8)^2 + ST^2`.

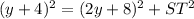Expand and simplify: Expanding the equation, we get:
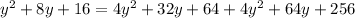`y^2 + 8y + 16 = 4y^2 + 32y + 64 + 4y^2 + 64y + 256`. Combining like terms, we get:
`-2y^2 - 24y - 224 = 0`.

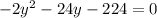Solve for y: We can use the quadratic formula to solve for
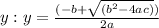`y: y = ( (-b +√((b^2 - 4ac))))/(2a)`. In this case, a = -2, b = -24, and c = -224. Solving for y, we get two possible values: y ≈ -7.32 or y ≈ 15.82.

Finding ST and TU:

Use the positive value of y: Since the side length cannot be negative, we take the positive value of y, which is y ≈ 15.82.

Find ST: Substitute y back into the expression for ST: ST = 2y + 8 ≈ 2(15.82) + 8 ≈ 41.64.

Find TU: Substitute y back into the expression for TU: TU = y + 4 ≈ 15.82 + 4 ≈ 19.82.

Therefore:

y ≈ 15.82

ST ≈ 41.64

TU ≈ 19.82