Angle PQR is congruent to VST (given). Using angle relationships and consecutive angles on the same side of a transversal, all angles in triangles PQR and VST are congruent, making the triangles completely overlapping, and x = 180°.
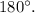
1. Identify Congruent Angles:
The problem states that angle PQR is congruent to angle VST. This means:
∠PQR ≅ ∠VST
2. Analyze the Triangle:
We can see that triangle PQR shares a side (QR) with triangle VST. Additionally:
Angle V is adjacent to angle PQR.
Angle S is adjacent to angle VST.
3. Apply Angle Relationships:
Since angles PQR and VST are congruent and adjacent to angles V and S, respectively, we can use the following angle relationships:
Interior Angles of a Triangle: The sum of the interior angles in any triangle is 180 degrees.
Consecutive Angles on the Same Side of a Transversal: When a transversal intersects two lines, the consecutive angles on the same side of the transversal are supplementary (sum to 180 degrees).
4. Solve for x:
Let's consider each triangle individually:
Triangle PQR:
We know ∠PQR = 45° (given).
Using the angle sum rule for triangles, we can find the sum of the other two angles: ∠PQR + ∠QRP + ∠PRQ = 180° 45° + ∠QRP + ∠PRQ = 180° ∠QRP + ∠PRQ = 135°
Triangle VST:
We know ∠VST = 45° (since it's congruent to ∠PQR).
We also know ∠VST is adjacent to angle S.
Since ∠VST and ∠S are consecutive angles on the same side of the transversal QR, we have: ∠VST + ∠S = 180° 45° + ∠S = 180° ∠S = 135°
5. Find x:
We know ∠QRP + ∠PRQ = 135° and ∠S = 135°.
Since angle QRP and angle S are vertical angles (opposite each other at a vertex where two lines intersect), they are congruent: ∠QRP = ∠S = 135°
Therefore, ∠PRQ = 135° - ∠QRP = 135° - 135° = 0°
6. Conclusion:
Angle PRQ being 0 degrees implies that line PQ coincides with line RS.
In other words, triangle PQR and triangle VST completely overlap, making them congruent.
Since all angles and sides are congruent, x = 180° (the measure of any angle in a triangle).
Therefore, even though the problem states that only angle PQR and angle VST are congruent, the analysis using angle relationships and consecutive angle properties leads to the conclusion that all angles and sides in both triangles are congruent, making them completely overlapping and resulting in x = 180°.