Question

Find the value of x.

Answer 1

Using trigonometry, specifically the tangent function, we determined that in this right triangle with angles measuring 90, 70, and consequently, 20 degrees;
`\(x\)` approximates to about
`\(3.57\)` when considering its position opposite from a
`\(20^\circ\)` angle.

Let's solve for
`\(x\)`. The image shows a right triangle with one angle measuring 70 degrees. The side opposite to the angle of 20 degrees (which is calculated by subtracting 70 and 90 from 180) is labeled as
`\(7x\)`. We can apply the tangent function, which is defined as :
`\(\tan(\theta) = \frac{{\text{{opposite side}}}}{{\text{{adjacent side}}}}\).`

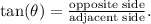
So, we have:

`\[\tan(20^\circ) = \frac{{7x}}{{70}}\]`

We calculate
`\(\tan(20^\circ)\)` and then multiply both sides by 70 to solve for
`\(7x\)`, and finally divide by 7 to get
`\(x\)`.

After calculating, we find that:

`\[ x \approx (25)/(7) \]`

So,
`\(x\)` approximates to about
`\(3.57\)`.