Question

What is the surface area of the cuboid below?

Answer 1

The surface area of a cuboid measuring
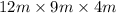`\(12 m * 9 m * 4 m\)` is calculated as
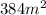`\(384 m^2\)`. This measure is vital in fields like engineering for material estimation.

The image presents a cuboid with given dimensions: length 12m, breadth 9m, and height 4m. The surface area of a cuboid is calculated using the formula
`\(2(lb + bh + lh)\)`, where l, b, and h represent the length, breadth, and height respectively. Substituting the given values into this formula gives us (2(12*9 + 9*4 + 12*4) = 2(108 + 36 +48) = 2(192) =
`384 m^2`.

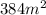The surface area is an essential aspect in various fields such as engineering, architecture, and physics. It helps in understanding how much material would be needed to cover the cuboid or in thermal dynamics; it can assist in determining how much heat will be lost or gained by a body. In this case of a cuboid with dimensions of length 12m, breadth 9m, and height of 4m; architects could use this information to estimate the amount of paint required to cover the exterior surface without wastage.

In mathematical terms, it provides an avenue for students and professionals alike to apply theoretical knowledge into practical scenarios enhancing comprehension and retention. It bridges abstract concepts making them tangible and relatable which is crucial for learning processes.