Question

The sides of a nuclear power plant cooling tower form a hyperbola. The diameter of the bottom of the tower is 288 feet. The smallest diameter of the tower is 150 which is 425 feet above the ground. The tower is 590 feet tall.

find width of tower at a height of 137 feet

Answer 1

The width of tower at a height of 137 feet is 401.4 feet

How to determine the width of tower at a height of 137 feet

From the question, we have the following parameters that can be used in our computation:

Diameter of the bottom = 288 feet

Smallest diameter = 150 feet

Height = 425 feet above the ground

Height of tower = 590 feet tall.

A hyperbola is represented as

`((x - h)^2)/(a^2) + ((y - k)^2)/(b^2) =1`

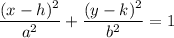
Using the given values, we have

`((x - 150)^2)/(288^2) + ((y - 425)^2)/(590^2) =1`

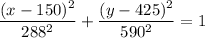
At a height of 137 feet, we have

`((x - 150)^2)/(288^2) + ((137 - 425)^2)/(590^2) =1`

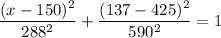
This gives

`((x - 150)^2)/(288^2) = 1 - ((137 - 425)^2)/(590^2)`

`((x - 150)^2)/(288^2) = 1 - (82944)/(348100)`

`((x - 150)^2)/(288^2) = (348100-82944)/(348100)`

`((x - 150)^2)/(288^2) = (265156)/(348100)`

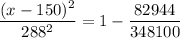
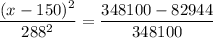
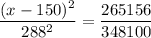
Take the square root of both sides

`(x - 150)/(288) = (515)/(590)`

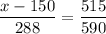
So, we have

x - 150 = 251.4

This gives

x = 401.4

Hence, the width of tower is 401.4 feet