The solution for (x) in f(x) = 400 for the function
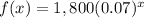 is obtained by setting up and solving the equation, resulting in
is obtained by setting up and solving the equation, resulting in
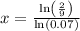 .
.
The given function is
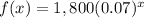 , and you're seeking to find (x) when f(x) = 400. Set (f(x)) to 400 and solve for (x):
, and you're seeking to find (x) when f(x) = 400. Set (f(x)) to 400 and solve for (x):
![\[400 = 1,800(0.07)^x\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/60fgzwow6k82530foyzter7mjr8fwfw8rt.png)
To isolate (x), divide both sides by 1,800:
![\[(400)/(1,800) = (0.07)^x\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/nkban7f5zkwgxdh0jgkrkspu969farmcl8.png)
Simplify the fraction:
![\[(2)/(9) = (0.07)^x\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/sk36k7ghrkswpbbpezkv0x7l7ro8riz5gp.png)
Take the natural logarithm (ln) of both sides:
![\[ \ln\left((2)/(9)\right) = x \cdot \ln(0.07) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yk60ldsby0cu09qr03jbvygixxllihjyyj.png)
Solve for (x):
![\[ x = (\ln\left((2)/(9)\right))/(\ln(0.07)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/oypoogmjw509qrdqselgfm535fpxlva9ry.png)
Using a calculator, evaluate this expression to find the numerical value of (x).
In summary, the solution to f(x) = 400 for the given function
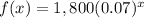 is
is
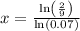 .
.