Question

WILL GIVE 35 POINTS

A map of an obstacle course is shown in the graph. The running path for the course is shaped like a right triangle where each unit is equal to 1 meter.

graph of a right triangle with points at negative 12 comma 0 labeled Obstacle 1, negative 12 comma 5 labeled Starting Point, and 0 comma 0 labeled Obstacle 2

Part A: Find the distance in meters from the starting point to obstacle 2. Show every step of your work. (3 points)

Part B: How many meters is one full lap around the course? Show every step of your work

Answer 1

A. The distance from the starting point to obstacle 2 is 10 meters.

B. One full lap around the course is 24 meters.

In order to determine the distance from the starting point to obstacle 2, we would apply Pythagorean's theorem by calculating the length of the hypotenuse of the right-angled triangle.

In Mathematics and Geometry, Pythagorean theorem is modeled or represented by the following formula:

`z^2=x^2 + y^2`

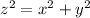
Where:

• x is the opposite side of a right-angled triangle.
• y is the adjacent side of a right-angled triangle.
• z is the hypotenuse of a right-angled triangle.

Part A.

By substituting the side lengths of the right-angled triangle, we have;

`z^2=x^2 + y^2 \\\\z^2=8^2 + 6^2 \\\\z^2=64+36\\\\z=√(100)`

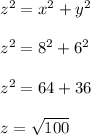
z = 10 meters.

Part B.

One full lap around the course can be determined by adding all of the side lengths of the right-angled triangle as follows;

One full lap = 8 + 6 + 10

One full lap = 24 meters.

Missing information:

A map of an obstacle course is shown in the graph. The running path for the course is shaped like a right triangle where each unit is equal to 1 meter.

Part A: Find the distance in meters from the starting point to obstacle 2. Show every step of your work. (3 points)

Part B: How many meters is one full lap around the course? Show every step of your work