Question

A portfolio consists of 35 percent of stock x and 65 percent of stock y. stock x is expected to return 15 percent if the economy booms, return 10 percent if it is normal, and lose 19 percent if it is recessionary. stock y will return 26 percent in a boom, return 15 percent in a normal economy, and lose 40 percent in a recession. the probability of a boom is 5 percent and probability of a recession is 10 percent. what is the portfolio standard deviation? multiple choice

a. 14.05%
b. 14.22%
c. 11.69%
d. 12.33%
e. 12.10%

Answer 1

The standard deviation of the portfolio is given as 14.05%

How to get the standard deviation of the portfloio

First, let's calculate the expected returns of Stock X and Stock Y in recession and the boom periods

`E(r)_{\text{Boom}} = (0.35 * 0.15) + (0.65 * 0.26) = 0.2215 \\`

`E(r)_{\text{Normal}} = (0.35 * 0.10) + (0.65 * 0.15) = 0.1325 \\`

`E(r)_{\text{Recession}} = 0.35(-0.19) + 0.65(-0.40) = -0.3265 \\`

`E(r)_{\text{Portfolio}} = 0.05(0.2215) + 0.85(0.1325) + 0.10(-0.3265) = 0.09105 \\`

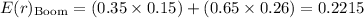
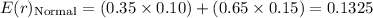
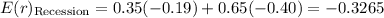
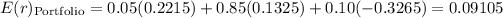
Calculate the portfolio standard deviation using the formula for a two-asset portfolio

`\sigma_{\text{Portfolio}} = \sqrt{0.05 \left[(0.2215 - 0.09105)^2\right]` +
`0.85 \left[(0.1325 - 0.09105)^2\right]` +
`0.10 \left[(-0.3265 - 0.09105)^2\right]}`

When we open the equation above we have:

= 14.05%