Question

If the chemical mass is 110.0 g/mol, what is its molecular formula?

Carbon mass is 17.900
Hydrogen mass is 1.680
Oxygen mass is 4.225
Nitrogen mass is 1.228

Answer 1

The molecular formula is
`\(C_5H_5NO\).`

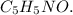
Carbon (C):

Moles of Carbon =
`\(\frac{17.900 \, \text{g}}{12.01 \, \text{g/mol}} \approx 1.491 \, \text{mol}\)`

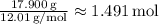
Hydrogen (H):

Moles of Hydrogen =
`\(\frac{1.680 \, \text{g}}{1.01 \, \text{g/mol}} \approx 1.667 \, \text{mol}\)`

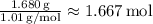
Oxygen (O):

Moles of Oxygen =
`\(\frac{4.225 \, \text{g}}{16.00 \, \text{g/mol}} \approx 0.264 \, \text{mol}\)`

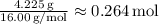
Nitrogen (N):

Moles of Nitrogen =
`\(\frac{1.228 \, \text{g}}{14.01 \, \text{g/mol}} \approx 0.087 \, \text{mol}\)`

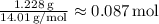
Next, find the ratio of moles:

The smallest mole value is approximately 0.087 mol (Nitrogen).

`\( \text{Carbon} : \text{Hydrogen} : \text{Oxygen} : \text{Nitrogen} \)`

\
`(1.491 : 1.667 : 0.264 : 0.087\)`

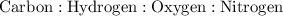
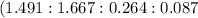
This equates to: 4 : 4 : 1 : 1

Therefore, the empirical formula is
`\(C_4H_4NO\)`.

Now, calculate the empirical formula mass:

`\[ \text{Empirical Formula Mass} = (4 * \text{Atomic Mass of C}) + (4 * \text{Atomic Mass of H}) + \text{Atomic Mass of N} + \text{Atomic Mass of O} \]`

`\[ \text{Empirical Formula Mass} = (4 * 12.01) + (4 * 1.01) + 14.01 + 16.00 \]`

`\[ \text{Empirical Formula Mass} = 48.04 + 4.04 + 14.01 + 16.00 \]`

`\[ \text{Empirical Formula Mass} = 82.09 \, \text{g/mol} \]`

To find the molecular formula, we need to compare the empirical formula mass (82.09 g/mol) with the given chemical mass (110.0 g/mol).

`\[ \text{Ratio} = \frac{\text{Given Chemical Mass}}{\text{Empirical Formula Mass}} \]`

`\[ \text{Ratio} = (110.0)/(82.09) \]` = 1.340

`\[ \text{Molecular Formula} = 1.340 * C_4H_4NO \]`

To obtain a whole number ratio, we can round the subscripts to the nearest whole number:

`\[ \text{Molecular Formula} \approx C_5H_5N_1O_1 \]`