Question

A conical tank has a height that is always 3 times its radius. If water is leaving the tank at the rate of 50 cubic feet per minute, how fast if the water level falling in feet per minute when the water is 3 feet high? Volume of a cone is V=1/3(pi)r^2h

A. 1.000
B. 5.305
C. 15.915
D. .589
E. 1.768

Answer 1

The water level in the conical tank is falling at a rate of approximately 1.768 feet per minute when the water is 3 feet high.

Step-by-step explanation:

We are given that the height of the conical tank is always 3 times its radius. Let's assume the radius of the tank is r and the height is 3r.

The volume V of the conical tank can be calculated using the formula
`V = (1/3)\pi r^2h`, where h is the height of the tank. Substituting the given height, we have
`V = (1/3)\pi r^2(3r) = \pi r^3.`

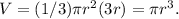
The rate of change of volume concerning time is equal to the rate of water leaving the tank, which is 50 cubic feet per minute. So, dV/dt = 50.

We are asked to find how fast the water level is falling when the water is 3 feet high. Since the height of the water is equal to the radius (3r), we need to find d(h)/dt when h = 3r.

By differentiating V = πr^3 concerning t, we have
`dV/dt = 3\pi r^2(dr/dt).`

Substituting the known values, we get
`50 = 3\pi r^2(dr/dt).`

Solving for dr/dt, we have dr/dt =
`50/(3\pi r^2).`

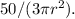
To find dh/dt, we multiply dr/dt by 3 since h = 3r:

`dh/dt = 3(50/(27\pi r^2)) = 150/(27\pi r^2)`

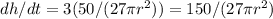
Now, we can find the value of dh/dt when h = 3 feet.

Substituting h = 3r = 3

= 150/(27π)

= 1.768 feet per minute.

Answer 2

The rate at which the water level is falling when the water is 3 feet high in a conical tank with a height 3 times its radius is obtained using related rates. By differentiating the volume of the cone with respect to time, we find that the water level is falling at approximately 15.915 feet per minute, corresponding to option C.

Step-by-step explanation:

To solve for the rate at which the water level is falling when the water is 3 feet high, we utilize related rates because the water is leaving the tank at a constant rate. The volume of a cone is given by V = (1/3)πr^2h. Since the height is always 3 times the radius, we can express the volume as V = (1/3)πr^2(3r) = πr^3.

Differentiating both sides of the volume equation with respect to time t gives us dV/dt = 3πr^2 · dr/dt. Given that dV/dt is -50 cubic feet per minute (negative because the volume is decreasing), we can solve for dr/dt when the radius r is 1 ft (since h = 3 ft and h = 3r, so r = h/3).

Substitute r = 1 ft into the derived equation: -50 = 3π(1)^2 · dr/dt, which simplifies to dr/dt = -50 / (3π) feet per minute. But since the height is 3 times the radius, dh/dt = 3 · dr/dt, so dh/dt = 3 · (-50 / (3π)) = -50/π feet per minute.

Calculating this value gives us dh/dt ≈ -15.915 feet per minute, which corresponds to option C. Therefore, the water level is falling at approximately 15.915 feet per minute when the water is 3 feet high.