Question

Jasmine needs to solve the quadratic equation: x2 2x – 2 = 6. Which statement about how Jasmine should solve this equation is true

Answer 1

The statement Jasmine should use the quadratic formula to find the values of
`\(x\)` is true. The correct answer is option B.

In the solution provided, we applied the quadratic formula to find the values of \(x\) for the given quadratic equation \(x^2 + 2x - 2 = 6\).

Let's solve the quadratic equation
`\(x^2 + 2x - 2 = 6\)` using the quadratic formula.

The quadratic formula is given by:

`\[ x = (-b \pm √(b^2 - 4ac))/(2a) \]`

For the given equation
`\(x^2 + 2x - 2 = 6\)`, we can identify
`\(a = 1\), \(b = 2\)`, and
`\(c = -8\)`.

Now plug these values into the quadratic formula:

`\[ x = (-2 \pm √(2^2 - 4(1)(-8)))/(2(1)) \]`

Simplify the expression under the square root:

`\[ x = (-2 \pm √(4 + 32))/(2) \]`

`\[ x = (-2 \pm √(36))/(2) \]`

`\[ x = (-2 \pm 6)/(2) \]`

Now, consider both the positive and negative square root:

1. For
`\( x = (-2 + 6)/(2) = 2 \)`

2. For
`\( x = (-2 - 6)/(2) = -4 \)`

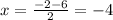
So, the solutions to the quadratic equation
`\(x^2 + 2x - 2 = 6\) are \(x = 2\) and \(x = -4\)`.
Therefore The statement Jasmine should use the quadratic formula to find the values of
`\(x\)` is true. The correct answer is option B.

The complete question could be

Which of the following statements is true about the correct method for Jasmine to solve the quadratic equation
`\(x^2 + 2x - 2 = 6\)` ?

A) Jasmine should factor the quadratic expression and set each factor equal to zero.

B) Jasmine should use the quadratic formula to find the values of
`\(x\)`.

C) Jasmine should complete the square to rewrite the equation in vertex form.

D) Jasmine should solve for
`\(x\)` by isolating the variable on one side of the equation using basic algebraic operations.

Choose the option that accurately represents the true approach for Jasmine to solve the given quadratic equation.