Question

Inflation causes things to cost more, and for our money to buy less (hence your grandparents saying "In my day, you could buy a cup of coffee for a nickel"). Suppose inflation decreases the value of money by 3% each year. In other words, if you have $1 this year, next year it will only buy you $0.97 worth of stuff. How much will $100 buy you in 15 years?

Answer 1

$63.32

Explanation:

To calculate the future value of money considering inflation, we can use the formula for compound interest in reverse. In this case, it's a decrease due to inflation, so we can use the formula:

`\sf FV = PV * (1 - r)^t`

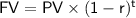
Where:

• 
  `\sf FV` is the future value (what $100 will buy in the future),
• 
  `\sf PV` is the present value (initial amount of money, $100 in this case),
• 
  `\sf r` is the rate of decrease due to inflation per year (3%, or 0.03 in decimal form), and
• 
  `\sf t` is the number of years (15 years in this case).

Now, substitute the values:

`\sf FV = 100 * (1 - 0.03)^(15)`

Calculate this expression to find the future value:

`\sf FV = 100 * (0.97)^(15)`

`\sf FV \approx 100 * 0.6332511891`

`\sf FV \approx 63.32511891`

`\sf FV \approx 63.32 \textsf{( in 2 d.p.)}`

Therefore, $100 will buy approximately $63.32 worth of goods in 15 years, considering a 3% annual decrease in the value of money due to inflation.