Question

Derivative of x^sqrt2

Answer 1

The derivative of x^sqrt2 is
`sqrt(2)x^(sqrt2-1).`

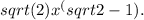
Let's find the derivative of the expression:

`$$(d)/(dx)(x^(√(2)))$$`

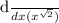
We can find the derivative of the expression using the power rule of differentiation, which states that the derivative of
`$x^n$ is $n\cdot x^(n-1)$ (where $n$ is any real number).`

The derivative of x^sqrt2 is sqrt(2)x^(sqrt2-1).

Start with the power rule for derivatives: If f(x) = x^n, then f'(x) = nx^(n-1).

Apply the power rule to the function x^sqrt2, where n = sqrt2. The derivative is sqrt(2)x^(sqrt2-1).

To find the derivative of x raised to the power of √2, which is x^sqrt2, we use the power rule for differentiation. The power rule states that the derivative of x^n is n*x^(n-1), where n is a constant. Therefore, the derivative of x^(√2) is √2*x^(√2-1).