Question

A tree leans precariously (or maybe impossibly) with its trunk making at an angle of /6 radians with the ground. The bottom end of a 10-foot ladder is 16 feet from the base of the trunk and the top end rests against the trunk. How far is the top end from the trunk's base? Solve this problem twice, once using the law of sines and then again using the law of cosines

Answer 1

The distance from the top end of the ladder to the base of the tree is approximately 8.92 feet.

Let's solve the problem using both the Law of Sines and the Law of Cosines.

Using the Law of Sines:

Let a be the length of the ladder, b be the distance from the bottom of the ladder to the base of the tree, and θ be the angle between the ladder and the ground.

The Law of Sines is given by:

`(sinA)/(a)` =
`(sinB)/(b)` =
`(sinC)/(c)`

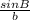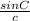
In this case, let A be the angle at the top of the ladder, B be the angle at the base of the tree, and C be the right angle (90 degrees).

`(sinA)/(a)` =
`(sinB)/(b)`

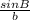
Now, we know that A=
`(π)/(6)` (in radians) and b=16 feet. We also know that a=10 feet.

`(sin(π)/(6) )/(10)` =
`(sin B)/(16)`

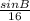
Solving for ⁡sin B:

sin B=
`(16(π)/(6) )/(10)`

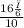
sin B=
`(8)/(5)`

Now, B=arcsin(
`(8)/(5)` ), but since the angle is between 0 and π, we discard the second solution.

Therefore,

B≈0.927 radians.

Now, the angle at the top of the ladder is
`(π)/(6)` radians, and the angle at the bottom is B≈0.927 radians. The remaining angle (C) is the right angle (90 degrees).

Using the Law of Cosines:

The Law of Cosines is given by:

`c^(2)`=
`a^(2)` +
`b^(2)` −2abcosC

In this case, c is the length of the ladder, a and b are the sides of the triangle formed by the ladder and the ground, and C is the angle between a and b (angle at the base of the tree).

`c^(2)` =
`10^(2)` +
`16^(2)` −2⋅10⋅16cos(
`(π)/(6)` )

`c^(2)` = 100+256−320cos (
`(π)/(6)` )

`c^(2)` =356−320⋅
`(√(3))/(2)`

`c^(2)` ≈356−276.39

c ≈
`√(79.61)`

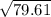
​c ≈ 8.92

So, using the Law of Sines, the distance from the top end of the ladder to the base of the tree is approximately 8.92 feet. This is the same result obtained using the Law of Cosines.