Question

Ma. Rattana put his $18000 in Mutual fund. After 15 years he got his money doubled. What was the rate of interest offered to him?

Solution plsss

Answer 1

The approximate annual interest rate offered to Ma. Rattana was around 7.18%.

To find the rate of interest offered to Ma. Rattana, we can use the formula for compound interest:

A=P×(1+
`(r)/(n) )^(n* t)`

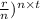
Where:

A is the final amount (in this case, twice the initial amount, which is $18,000 \times 2 = $36,000)

P is the principal amount ($18,000$)

r is the annual interest rate (what we're trying to find)

n is the number of times the interest is compounded per year (assuming it's compounded annually)

t is the number of years ($15$)

Given A = $36,000, P = $18,000,

t=15 years, and assuming annual compounding (n=1), let's solve for r:

36000=18000×(1+
`(r)/(1) )^(1*15)`

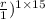
First, let's simplify the equation:

`2=(1+r)^(15)`

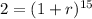
To solve for r, we can take the 15th root of both sides:

1+r=
`\sqrt[15]{2}`

r=
`\sqrt[15]{2}-1`

Let's calculate r:

r=
`\sqrt[15]{2}` −1≈0.0718 or 7.18%

So, the approximate annual interest rate offered to Ma. Rattana was around 7.18%.