Answer:
≈ 0.8 m²
Explanation:
________________________________________________
FORMULA FOR FINDING AREA OF SEGMENT :-
![A = r^(2) [(\alpha )/(360) * \pi - (\sin (\alpha )/(2) * \cos (\alpha )/(2) )]](https://img.qammunity.org/2022/formulas/mathematics/high-school/vv9hv3f0sb0mqk3h69qp53nrhtwxzpl150.png)
Where :-
- A = Area of the segment
- r = Radius of the circle
- α (alpha) = Angle subtended by arc at the center
________________________________________________
Angle subtended by the minor arc at the center = 360° - 300° = 60°
Radius of the circle = 3 m
Area of the segment =
![3^(2) [ (60)/(360) * \pi - (\sin (60)/(2) * \cos (60)/(2))]](https://img.qammunity.org/2022/formulas/mathematics/high-school/yname2s124jqmmojm6cqhc4cpz9o3bqei8.png)
![= 9[(1)/(6) * \pi - (\sin 30 * \cos 30)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/botralq92u353t078vnhk0ikthe8axh42k.png)
![= 9[(\pi )/(6) - ((1)/(2) * (√(3) )/(2) )]](https://img.qammunity.org/2022/formulas/mathematics/high-school/2ygj6tdev3utgooci3qu39fqusu4eou24d.png)
![= 9[(\pi )/(6) - (√(3) )/(4) ]](https://img.qammunity.org/2022/formulas/mathematics/high-school/egfjekm65qx12069iehckstw1omvd6jz0y.png)
![= 9[(2\pi - 3√(3) )/(12) ]](https://img.qammunity.org/2022/formulas/mathematics/high-school/43shzuhg02r389te8akwu4v3gyj0my9p6y.png)
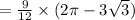
( Assuming √3 = 1.73 & π = 3.14 )
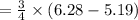
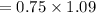
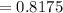
∴ Area of the segment ≈ 0.8 m² (rounding to the nearest tenth)