Question

+

2
2
-2
N
4
x
Solve the system of equations algebraically. Verify your
answer using the graph.
y = 4x - 5
y=-3
What is the solution to the system of equations?
0 (4,-3)
0(2,-3)
(-3,2)
O

Answer 1

The solution to the system of equations is
`\( (x, y) = \left((1)/(2), -3\right). \)`

Let's solve the system of equations algebraically:

1. Equation 1: y = 4x - 5

2. Equation 2: y = -3

To find the solution, set the right-hand sides of the equations equal to each other:

4x - 5 = -3

Now, solve for x :

4x = -3 + 5

4x = 2

`\[ x = (2)/(4) \]`

`\[ x = (1)/(2) \]`

Now that we have
`\( x = (1)/(2) \)`, substitute it back into either equation to find
y. Let's use Equation 1:

`\[ y = 4 * (1)/(2) - 5 \]`

y = 2 - 5

y = -3

So, the solution to the system is
`\( (x, y) = \left((1)/(2), -3\right) \)`.

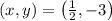Now, let's verify this solution using the graph:

The point
`\( \left((1)/(2), -3\right) \)` should satisfy both equations. When you substitute

`\( x = (1)/(2) \)` and y = -3 into the original equations, both should be true. Verify this to confirm the solution.