Question

Let f(x)=x^3/6+10+1/2x. Calculate the arc length of the graph of f(x) over the interval [2,5].

Enter an exact answer.

Answer 1

The exact arc length of the graph of f(x)=x^3/6+10+1/2x over the interval [2,5] is
`√(625) /3+169√(13) /6`.

The arc length L of a function f(x) over an interval [a,b] is given by the integral:

`L=\int\limits^a_b {1+[f'(x)]^2 dx`

where f' (x) is the derivative of f(x). In this case,

Now,
`f'(x)=1/2x^2+1/2`

Now, substitute f' (x) into the arc length formula and integrate over the interval [2, 5]:

`L=\int\limits^5_2 {√(1+(1/2x^2+1/2)^2) } \, dx`

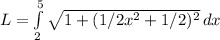
Simplify the expression inside the square root:

`L=\int\limits^5_2 {√(1/4x^4+1/2x^2+5/4) } \, dx`

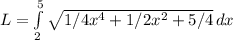
Now, integrate with respect to x. The result is the exact expression:

`L=√(625) /3+169√(13) /6`

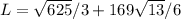
This is the exact arc length of the graph of f(x) over the interval [2, 5].