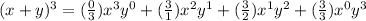Question

In this activity, you'll use the binomial theorem to find the expanded form of a binomial expression. Answer the following

questions using the binomial theorem.
(a + b)" = a² + a²-¹b² + "(n-¹) an-26² + n(n-1)(n-2) an-3f³ + ...
· +6"
Question 1
? Question
Use
the binomial theorem to determine the expanded form of the binomial expression (x + y)¹.
2 + y²
+ 2z³y + 3x³y² + 2xy + y
Expanded Form
z + 4z³y + 6x³y² + 4xy³+ y
z¹+z³y + z³y² + 2y³ + y²

Answer 1

The expanded form of
`(x+y)^3 = x^3 +3x^2y+3xy^2+y^3`.

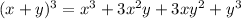The binomial theorem states that
`(a+b)^n = \sum^n_(k=0)((n)/(k))a^(n-k)b^k`, where
`((n)/(k) )`

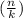
represents the binomial coefficient, which is calculated as
`(n!)/(k!(n-k)) .`

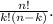
Let's find the expanded form of the binomial expression
`(x+y)^3`.

`(x+y)^3 = ((0)/(3) )x^3y^0+((3)/(1) )x^2y^1+((3)/(2) )x^1y^2+((3)/(3) )x^0y^3`

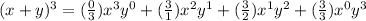
Solving the binomial coefficients:

`((3)/(0) )= 1\\((3)/(1) )= 3\\((3)/(2) )= 3\\((3)/(3) )= 1`

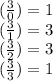
Now, let's plug these into the expanded form:

`(x+y)^3 = x^3 +3x^2y+3xy^2+y^3`

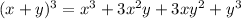
Therefore, the expanded form of
`(x+y)^3 = x^3 +3x^2y+3xy^2+y^3`.

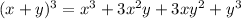Question

The binomial theorem to determine the expanded form of the binomial expression
`(x+y)^3 = ((0)/(3) )x^3y^0+((3)/(1) )x^2y^1+((3)/(2) )x^1y^2+((3)/(3) )x^0y^3`