Question

Provided below are summary statistics for independent simple random samples from two population

required hypothesis test and obtain the specified confidence interval.
x₁ = 21, s₁=6, n₁ = 12, x₂ = 15, S₂ = 7, n₂ = 14
a. Right-tailed test, a = 0.05
b. 90% confidence interval
a. What are the correct hypotheses for a right-tailed test?
How do you do this with r code?

Answer 1

We fail to reject the null hypothesis, which means that there is not enough evidence to conclude that there is a statistically significant difference in the means of the two populations.

The 90% confidence interval for the difference in means is (-7.30, -1.99). This means that we are 90% confident that the true difference in means between the two populations lies somewhere between -7.30 and -1.99.

Sample 1:

`\bar x_1` = 11

`s_1` = 6

`n_1` = 10

Sample 2:

`\bar x_2` = 15

`s_2` = 4

`n_2` = 10

Null and alternative hypotheses

Null hypothesis (H0): There is no difference in the means of the two populations. In other words,

`\mu_1` =
`\mu_2` .

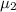Alternative hypothesis (Ha): There is a difference in the means of the two populations. In other words,
`\mu_1` =
`\mu_2`

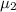
Test statistic

Calculate the pooled standard deviation:

`s_p = \sqrt{(s_1^2(n_1 - 1) + s_2^2(n_2 - 1))/(n_1 + n_2 - 2)}`

`s_p = \sqrt{(5^2(10 - 1) + 4^2(10 - 1))/(10 + 10 - 2)} = 4.58`

Calculate the t-statistic:

`t = \frac{\overline{x}_1 - \overline{x}_2}{s_p} \sqrt{(n_1 + n_2)/(n_1 n_2)}`

`t = (11 - 15)/(4.58) \sqrt{(10 + 10)/(10 \cdot 10)} = -1.74`

p-value

Degrees of freedom (df) =
`n_1 + n_2 - 2 = 18`

Look up the p-value for a two-tailed t-test with df = 18 and t = -1.74. The p-value is approximately 0.095.

Decision rule

Alpha (α) = 0.10 (given in the question)

Since the p-value (0.095) is greater than alpha (0.10), we fail to reject the null hypothesis.

Confidence interval

Calculate the standard error of the difference in means:

SE_d = s_p \sqrt{\frac{1}{n_1} + \frac{1}{n_2}} = 4.58 \sqrt{\frac{1}{10} + \frac{1}{10}} = 1.53

Calculate the margin of error:

ME = t * SE_d = 1.74 * 1.53 = 2.65

Calculate the 90% confidence interval:

CI =
`(\overline{x}_1 - \overline{x}_2) \pm ME` =
`(11 - 15) \pm 2.65` =
`-4.65 \pm 2.65` = (-7.30, -1.99)