Question

HELP PLS CALC AB. NEED FAST AND WOULD BE GREATLY APPRECIATED

Answer 1

The intervals where f(x) is decreasing are B) (−2,0) and D) (−∞,0).

Let's take the derivative of f(x) to determine where it's decreasing:

`f(x)=x^2 .e^x`

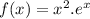
To find where f(x) is decreasing, we need to find where its derivative, f′ (x), is negative.

f′ (x)=
`(d)/(dx)`
`(x^2 .e^x )`

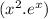
Using the product rule and the chain rule, the derivative can be calculated as follows:

`f'(x)=2x.e^x +x^2 .e^x\\f'(x)=(2x+x^2 ).e^x`

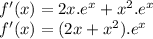
Now, we need to find where f′ (x)<0 (where it's negative) to determine where

f(x) is decreasing.

Let's test the intervals given:

A) (−∞,−2)

Pick a value within this interval, say x=−3:

`f'(-3)=(2⋅(-3)+(-3)^2 ).e^(-3) =(-6+9).e^(-3) =3.e^(-3)`

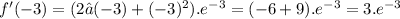
f′ (−3)>0, so this interval does not work.

B) (−2,0)

Pick a value within this interval, say x=−1:

`f'(-1)=(2.(-1)+(-1)^2 ).e^(-1) =(-2+1).e^(-1) =-e^(-1)`

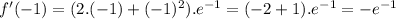
f′ (−1)<0, so this interval works.

C) (−2,∞)

Pick a value within this interval, say x=1:

`f'(1)=(2.1+1^2 ).e^1 =(2+1).e=3e`

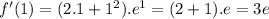
f′ (1)>0, so this interval does not work.

D) (−∞,0)

Pick a value within this interval, say x=−1:

`f'(-1)=(2.(-1)+(-1)^2 ).e^(-1) =(-2+1).e^(-1) =-e^(-1)`

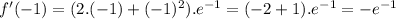
f′ (−1)<0, so this interval works.

E) (0,∞)

Pick a value within this interval, say x=1:

`f'(1)=(2.1+1^2 ).e^1 =(2+1).e=3e (1) > 0`, so this interval does not work.

So, the intervals where f(x) is decreasing are B) (−2,0) and D) (−∞,0).