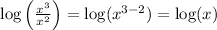Question

Simplify the following expression. log(x3) - log(x2)

Answer 1

log(x)

Step-by-step explanation:

Using logarithm properties, we can simplify the expression
`(\log(x^3) - \log(x^2)`

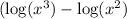
The properties of logarithms state that subtracting logarithms with the same base is equivalent to dividing their arguments:

`\log_b(a) - \log_b(c) = \log_b\left((a)/(c)\right)`

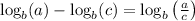
Applying this to the given expression:

`\log(x^3) - \log(x^2) = \log\left((x^3)/(x^2)\right)`

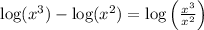
Now, using the properties of exponents
`(x^a / x^b = x^(a - b))`

`\log\left((x^3)/(x^2)\right) = \log(x^(3-2)) = \log(x)`