Question

34) x = y³, y =1/x. x= 1, and
y = 2

rotated around the x-axis.

Answer 1

The volume of the solid generated by rotating the curve
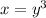`x=y^3` around the x-axis when x=1 and y=1 is π cubic units.

Let's start by understanding the given equations:

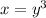
`x=y^3`

y=
`(1)/(x)`

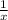
​We're given two equations, but we also have specific values for x and y:

x=1 and y=2.

From equation 2, when y=2, x=
`(1)/(y)` =
`(1)/(2)` . This doesn't align with the x=1 provided, so let's recheck the information.

If x=1, using equation 1, we can find y by substituting x=1 into the equation:

`x=y^3\\1=y^3\\y=1`

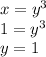
Therefore, when x=1, y=1.

Now, we're rotating the curve defined by these equations around the x-axis. The equation x=y^3 describes a curve in the xy plane. When we rotate this curve around the x-axis, we get a three-dimensional shape.

The rotation of the curve around the x-axis generates a solid shape that can be calculated using integration. The formula to find the volume of a solid of revolution when rotating a curve around the x-axis is given by:

V=π
`\int\limits^b_a {(f(x))^2} \, dx`

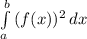
where

f(x) represents the curve's function.

For the curve x=y^3

where

y=1 when x=1, the shape generated by rotating around the x-axis can be calculated by integrating from x=0 to x=1 using
`f(x)=(1)^2 =1` because the rotation is around the x-axis.

V=π
`\int\limits^1_0 {1} \, dx`

V=π
`[x]^1_0`

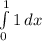
V=π(1−0)

V=π

So, the volume of the solid generated by rotating the curve x=y^3 around the x-axis when x=1 and y=1 is π cubic units.