Question

Use differentials to estimate the amount of tin in a closed tin can with diameter 10 cm and height 13 cm if the tin is 0.04 cm thick. (Round your answer to two decimal places.)

Answer 1

The estimated amount of tin added to the can due to the thickness is approximately 4.42 cubic centimeters.

To estimate the amount of tin in the closed tin can, we can use differentials. Let r be the radius of the can, h be the height, and t be the thickness of the tin.

The volume V of the tin can is given by the formula
`\( V = \pi r^2 h \)`. To find the differential dV , we can take the derivative with respect to r:

`\[ dV = 2\pi rh \, dr + \pi r^2 \, dh \]`

Now, we substitute the given values: r = 5 ,
`\text{cm} \)`, h = 13,
`\text{cm} \),`
`\( dr = dt \)`(small change in radius), and dh = dt (small change in height). Also,
`\( t = 0.04 \, \text{cm} \).`

`\[ dV = 2\pi \cdot 5 \cdot 13 \, dt + \pi \cdot 5^2 \, dt \]`

Simplifying, we get
`\( dV = 330\pi \,`
`dt + 25\pi \,`
`dt = 355\pi \, dt \).`

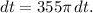
This differential dV represents the change in volume. To estimate the change in volume due to the change in thickness, we can multiply dV by the thickness t :

`\[ \Delta V \approx dV \cdot t = 355\pi \cdot 0.04 \, dt \]`

Now, we can evaluate this expression. Using
`\( \pi \approx 3.14 \)`, we find
`\( \Delta V \approx 4.42 \, dt \)` cubic centimeters.

Therefore, the estimated amount of tin added to the can due to the thickness is approximately 4.42 cubic centimeters.