Question

Ive attached the photo this is bc calculus improper fractions​

Answer 1

The original integral converges for p > -1/3.

Sure, I can help with this. The integral in the question converges for values of p greater than -1/3. This can be seen by using the p -integral test. The p -integral test states that if
`$f(x) \ge 0$ for $x \ge a$` and
`$ \int_a^(\infty) f(x) x^p \,dx$` converges/diverges, then the integral
`$ \int_a^(\infty) f(x) \,dx$` converges/diverges as well.

In the case of the integral in the question,
`$f(x) = (1)/(x^(3p+1))$` and a = 1. We can see that
`$f(x) \ge 0$ for $x \ge 1$ and $p \ge -1/3$.` Let's plug these values into the p -integral test:

`$$\begin{aligned} \int_1^(\infty) f(x) x^p \,dx &= \int_1^(\infty) (1)/(x^(3p+1)) x^p \,dx \\ \\ &= \int_1^(\infty) x^(-p-1) \,dx \end{aligned}$$`

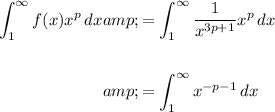
This integral converges for p > -1 (using the p -test again). Therefore, the original integral converges for p > -1/3.

Here are the answer choices and why they are correct or incorrect:

A. p < 0: This is incorrect because the integral converges for p = -1/3.

B. p > -1/3: This is correct, as we have shown above.

C. p > 0: This is incorrect because the integral converges for p = 0.

D. p > 1: This is incorrect because the integral converges for p = 1.