Question

One of the dangers for the orbiting International Space Station is orbiting debris. A meteoroid of mass 1.00 x 102 kg goes into a circular orbit about the earth in the same orbit as the International space station. The ISS is 340 km above the earth which has a radius of 6340 km. What is the speed of this meteoroid? [4 points] Me = 5.96 × 1024 kg

Answer 1

To find the speed of a meteoroid in the same orbit as the ISS, use the orbital velocity formula with the given Earth's mass and the total distance from Earth's center to the meteoroid. The calculated speed is approximately 7.67 km/s.

To calculate the speed of the meteoroid in the same orbital path as the International Space Station (ISS), we use the formula for orbital velocity:

`\[v = \sqrt{(G * M_e)/(r)}\]`

Where:

`\(G\)` is the gravitational constant
`(\(6.674 * 10^(-11) \, \text{m}^3 \, \text{kg}^(-1) \, \text{s}^(-2)\))`,

`\(M_e\)` is the mass of the Earth
`(\(5.96 * 10^(24) \, \text{kg}\))`,

`\(r\)` is the distance from the center of the Earth to the object (Earth's radius + altitude above Earth).

Given that the ISS is 340 km above Earth's surface and Earth's radius is 6340 km, we have
`\(r = 6680 \, \text{km}\) or \(6.68 * 10^(6) \, \text{m}\).`

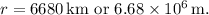
Substituting these values into the formula:

`\[v = \sqrt{\frac{(6.674 * 10^(-11) \, \text{m}^3 \, \text{kg}^(-1) \, \text{s}^(-2)) * (5.96 * 10^(24) \, \text{kg})}{6.68 * 10^(6) \, \text{m}}}\]`

Calculating the square root:

`\[v \approx 7.67 \, \text{km/s}\]`

Therefore, the meteoroid would be traveling at a speed of approximately 7.67 kilometers per second in the same orbit as the ISS. This is the orbital velocity required to stay in a stable orbit at that altitude above Earth.