Answer:
The area of an equilateral triangle is:
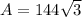 cm²
cm²
Hence, the left bottom option i.e.
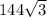 cm² is the correct option.
cm² is the correct option.
Explanation:
We know that the perimeter of a triangle is just the sum of its three sides.
Given that the perimeter of an equilateral triangle is 72cm.
i.e.
 cm
cm
Important Tip:
- We can determine the length of an individual side by dividing the perimeter of an equilateral triangle by 3 as all three sides of an equilateral triangle have the same length.
Let 'a' be the length of an individual side of an equilateral triangle.
The length of an individual side of an equilateral triangle will be:
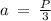
 ∵ The perimeter
∵ The perimeter

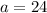 cm
cm
Thus,
The length of an individual side of an equilateral triangle: a = 24 cm
The area of an equilateral triangle can be determined using the formula
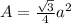
where 'a' is the length of an individual side
now substitute a = 24 cm in the formula

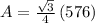 ∵ 24² = 576
∵ 24² = 576
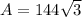 cm² ∵
cm² ∵
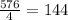
Therefore, the area of an equilateral triangle is:
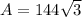 cm²
cm²
Hence, the left bottom option i.e.
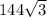 cm² is the correct option.
cm² is the correct option.