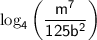Question

Explain how to simplify in one sentence

Answer 1

The simplified expression is
`log_4((m^7)/(125-b^2) ).`

let's simplify the expression step by step:

`7log_4 m- 3log_4 5 - 2log_4b^2`

Using logarithm properties:

`log_4 m- log_4 5^3 - log_4b^2`

Further simplification:

`log_4 m^7- log_4 125 - log_4b^2`

Combining logarithms:

`log_4((m^7)/(125-b^2) ).`

So, the simplified expression is
`log_4((m^7)/(125-b^2) ).`

Answer 2

`\sf \log_4 \left((m^7)/(125b^2)\right)`

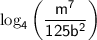
Explanation:

To simplify the expression
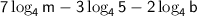`\sf 7\log_4 m - 3\log_4 5 - 2\log_4 b`, we can use the properties of logarithms. Here are some logarithmic properties that will be helpful:

`\boxed{\boxed{\begin{aligned} \log_b a + \log_b c & = \log_b (ac)\textsf{ (Product Rule)}\\\\ \log_b a - \log_b c & = \log_b \left((a)/(c)\right)\textsf{ (Quotient Rule)} \\\\ n \cdot \log_b a & = \log_b (a^n)\textsf{(Power Rule)}\end{aligned}}}`

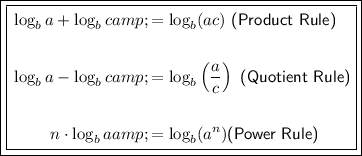
Applying these rules to the given expression:

`\sf 7\log_4 m - 3\log_4 5 - 2\log_4 b`

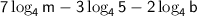
Using the Power Rule, we can bring the coefficients as exponents:

`\sf \log_4 m^7 - \log_4 5^3 - \log_4 b^2`

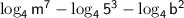
Now, apply the Product and Quotient Rules:

`\sf \log_4 \left((m^7)/(5^3 \cdot b^2)\right)`

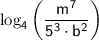
So, the simplified form of
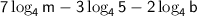`\sf 7\log_4 m - 3\log_4 5 - 2\log_4 b` is:

`\sf \log_4 \left((m^7)/(125b^2)\right)`