Question

Volume of the rectanglar Prism 3 2/3 4/5

Answer 1

The volume of the rectangular prism is
`\(96.8\)` cubic units.

To find the volume of a rectangular prism, you multiply the length, width, and height. If the dimensions are given as mixed numbers, you need to convert them to improper fractions.

Let's assume the dimensions of the rectangular prism are:

Length =
`\(3 (2)/(3)\)`

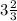
Width =
`\(4 (4)/(5)\)`

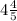
Height =
`\(5 (1)/(2)\)`

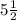
Now, convert the mixed numbers to improper fractions:

`\[\text{Length} = ((3 * 3) + 2)/(3) = (11)/(3)\]`

`\[\text{Width} = ((4 * 5) + 4)/(5) = (24)/(5)\]`

`\[\text{Height} = ((5 * 2) + 1)/(2) = (11)/(2)\]`

Now, multiply these fractions to find the volume:

`\[\text{Volume} = \text{Length} * \text{Width} * \text{Height} = (11)/(3) * (24)/(5) * (11)/(2)\]`

To simplify the result, you can cancel out common factors in the numerators and denominators:

`\[\text{Volume} = (11 * 24 * 11)/(3 * 5 * 2)\]`

Now, calculate the numerator and denominator separately:

Numerator:
`\(11 * 24 * 11 = 2904\)`

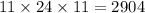
Denominator:
`\(3 * 5 * 2 = 30\)`

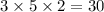
So, the simplified volume is:

`\[\text{Volume} = (2904)/(30) = 96.8\]`

Therefore, the volume of the rectangular prism is
`\(96.8\)`cubic units.