This rational function has a horizontal asymptote at y=3, a vertical asymptote at x=−2, and a hole at (−1,1).
To create a rational function with the specified characteristics, we need a rational expression that has a vertical asymptote at x=−2, a horizontal asymptote at y=3, and a hole at (−1,1). The general form of a rational function is:
f(x)=
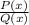
where
P(x) and Q(x) are polynomials.
For the vertical asymptote at x=−2, we need Q(x) to have a factor of (x+2) in the denominator. For the horizontal asymptote at y=3, the degree of P(x) and Q(x) should be the same.
Let's say P(x) and Q(x) are both quadratic polynomials, and Q(x) has a factor of (x+2). We can represent P(x) as a quadratic polynomial and divide by Q(x) to find the general form:
f(x)=

Now, let's find the values of a, b, c, d, and e such that the function has a hole at (−1,1). Since the hole occurs at x=−1, we need to ensure that (x+1) is a factor in both P(x) and Q(x). To create a hole at (−1,1), we can set P(−1)=Q(−1)=0.
Let's say P(x)=(x+1) (to create the hole) and Q(x)=(x+1)(x+2) (to have the vertical asymptote at x=−2). We can then simplify and adjust the coefficients to meet the requirements:
f(x)=
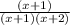
f(x)=
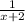
This rational function has a horizontal asymptote at y=3, a vertical asymptote at x=−2, and a hole at (−1,1).
Question
Write an equation of a rational function that has a horizontal asymptote at y = 3 and a vertical asymptote at x = −2 and a hole at (-1, 1).