Question

Solve system of equations 9X +11y and 3X plus 4Y equals 4

Answer 1

The solution to the system of equations
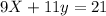`\(9X + 11y = 21\)` and
`\(3X + 4Y = 4\) is \(X = 16\) and \(Y = -9\).`

Certainly! Let's solve the system of equations:

1.
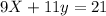
`\(9X + 11y = 21\)`

2.
`\(3X + 4Y = 4\)`

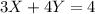
We can use various methods such as substitution, elimination, or matrices to solve this system. I'll use the substitution method here:

From equation (2), we can express \(X\) in terms of \(Y\):

`\[3X + 4Y = 4\]`

`\[3X = 4 - 4Y\]`

`\[X = (4 - 4Y)/(3)\]`

Now, substitute this expression for \(X\) into equation (1):

`\[9\left((4 - 4Y)/(3)\right) + 11Y = 21\]`

To simplify, multiply both sides by 3 to get rid of the fraction:

`\[9(4 - 4Y) + 33Y = 63\]`

Distribute and combine like terms:

`\[36 - 36Y + 33Y = 63\]`

`\[-3Y = 27\]`

Divide by -3 to solve for \(Y\):

`\[Y = -9\]`

Now that we have the value for \(Y\), substitute it back into the expression we found for \(X\):

`\[X = (4 - 4(-9))/(3) = 16\]`

So, the solution to the system of equations is
`\(X = 16\) and \(Y = -9\).`

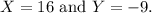
The probable question maybe:

Sure, let's consider the following system of equations:

1.
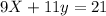
`\(9X + 11y = 21\)`

2.
`\(3X + 4Y = 4\)`

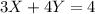
Now, you can try to solve this system of equations to find the values of \(X\) and \(Y\) that satisfy both equations. Feel free to go ahead and solve it, or let me know if you'd like me to assist you with the solution.