Question

X^2+4y-4x-24y+4=0
Ellipses

Answer 1

The given equation represents an ellipse with center (2, 6), semi-major axis of length 2√6, and semi-minor axis of length 26.

The given equation x² + 4y - 4x24y+4=0 can be rearranged to represent an ellipse.

The standard form of the equation for an ellipse is:

`((x-h)^2)/(a^2) +((y-k)^2)/(b^2) =1`

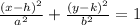
where (h, k) is the center of the ellipse, a is the length of the semi-major axis, and b is the length of the semi-minor axis.

To rewrite the given equation in standard form, complete the square for both 2 and y:

x²-4x+4+4y24y+4= 24

(x-2)²+4(y-6) = 24

Now, divide both sides by 24 to get the standard form:

`((x-2)^2)/(24) +((y-6)^2)/(6) =1`

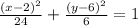
So, the given equation represents an ellipse with center (2, 6), semi-major axis of length 2√6, and semi-minor axis of length 26.

Question

Find the centre, the lengths of the axes, eccentricity, foci of the following ellipse:x^2+4y-4x-24y+4=0