Question

A rectangular plot, 19 ft by 20 ft, is to be used for a garden. It is decided to put a pavement inside the entire border so that 90 square feet of the plot is left for flowers. How wide should the pavement be?

Answer 1

The pavement should be 5 ft wide on each side.

Here's how to find the pavement width:

1. Calculate the total area of the plot:

Area of plot = length * width = 19 ft * 20 ft = 380 sq ft

2. Subtract the area left for flowers:

Area for pavement = Total area - Area for flowers = 380 sq ft - 90 sq ft = 290 sq ft

3. Treat the pavement as a rectangle within the main plot:

Let's call the pavement width "x". Therefore, the length of the inner rectangle (garden area) will be 20 ft - 2x (accounting for pavement on both sides).

4. Calculate the area of the inner rectangle:

Area of garden = Length * Width = (20 ft - 2x) * x

5. Set the area of the garden equal to the remaining area for pavement:

Area of garden = Area for pavement

(20 ft - 2x) * x = 290 sq ft

6. Solve the equation for x (pavement width):

Expand the left side:
`20x - 2x^2 = 290 sq ft`

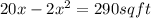
Move all terms to one side:
`2x^2 - 20x + 290 = 0`

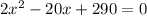
Factor the equation: (2x - 14)(x - 20) = 0

Therefore, x = 7 or x = 10.

7. Analyze the solutions

- x = 7: This would create a pavement 7 ft wide on each side, leaving a garden area of only 6 ft wide. This seems unlikely for a practical garden layout.

- x = 10: This creates a more reasonable pavement width of 5 ft on each side, resulting in a garden area of 10 ft wide.

Therefore, the pavement should be 5 ft wide on each side.