Question

A wind turbine uses the power of wind to generate electricity. The blades of the turbine make a

noise that can be heard at a distance from the turbine. At a distance of d = 0 meters from the
turbine, the noise level is 105 decibels. At a distance of d = 100 meters from the turbine, the
noise level is 49 decibels.
The noise level can be modeled by the function S given by S(d) = ab", where Sd) is the
noise level, in decibels, at a distance of d meters from the turbine.
Part C
Use the model S to find the value of m such that the noise level is 20 decibels at a distance of m meters from the turbine.

Answer 1

(1) Equations:
`\(S(0) = 105 = a\)` and S(100) = 49 =
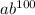`ab^(100)\)`. (2) Values: a = 105 and
`\(b \approx 0.9709\)`.

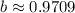Let's use the given data to write two equations and then solve for the constants a and b.

The general form of the model is
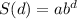`\(S(d) = ab^d\)`, where S(d) is the noise level in decibels at a distance d from the turbine.

1. Equation 1 using the point (0, 105):

When
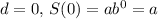`\(d = 0\), \(S(0) = ab^0 = a\)`, so at d = 0, the noise level is a decibels.

Therefore, a = 105.

Equation 1:

`\[S(0) = 105 = ab^0 = a\]`

2. Equation 2 using the point (100, 49):

When
`\(d = 100\), \(S(100) = ab^(100) = 49\)`.

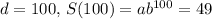Therefore,
`\(ab^(100) = 49\).`

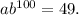
Equation 2:

`\[S(100) = 49 = ab^(100)\]`

Now we have a system of two equations:

`\[\begin{align*}1. & \quad a = 105 \\2. & \quad ab^(100) = 49 \\\end{align*}\]`

Let's solve for b using equation 2:

`\[105b^(100) = 49\]`

Now, divide both sides by 105:

`\[b^(100) = (49)/(105)\]`

Take the 100th root of both sides:

`\[b = \left((49)/(105)\right)^{(1)/(100)}\]`

Now you can calculate the values for b. Once you have b, you can substitute it back into equation 1 to find the value for a.

Let's finish the calculations:

From the previous steps, we found:

`\[ b = \left((49)/(105)\right)^{(1)/(100)} \]`

Now, let's calculate the value of b:

`\[ b \approx 0.9709 \]`

Now that we have the value for b, we can substitute it back into Equation 1 to find a:

a = 105

So, the values for the constants are:

`\[ a = 105 \]\[ b \approx 0.9709 \]`

Therefore, the model for the noise level S(d) in decibels at a distance d from the turbine is:

`\[ S(d) = 105 * (0.9709)^d \]`

The complete question is:

A wind turbine uses the power of wind to generate electricity. The blades of the turbine make a noise that can be heard at a distance from the turbine. At a distance of d = 0 from the turbine, the noise level is 105 decibels. At a distance of d = 100 meters from the turbine, the noise level is 49 decibels. The house level can be modeled by the function S is given by S(d) = ab^d , where S(d) is the noise level, in decibels, at a distance of d meters from the turbine

(1) Use the given data to write two equations that can be used to find the values for constants a and b in the expression for S(d).

(1) Find the values for a and b