Question

A random sample of 56 credit-card holders showed that 41 regularly paid their credit-card bills on time. Find a 90% confidence interval for p.

Answer 1

The 90% confidence interval for the population proportion p of credit-card holders regularly paying bills on time is approximately 0.637 to 0.827, based on a random sample of 56 credit-card holders.

To find the confidence interval for a population proportion (p), we can use the formula:

`\[ \text{Confidence Interval} = \hat{p} \pm z * \sqrt{\frac{\hat{p}(1 - \hat{p})}{n}} \]`

where:

-
`\(\hat{p}\)` is the sample proportion,

- z is the z-score corresponding to the desired confidence level,

- n is the sample size.

In this case, the sample proportion
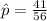`\(\hat{p} = (41)/(56)\)`, the sample size n = 56, and for a 90% confidence interval, the z-score is approximately 1.645.

`\[ \text{Confidence Interval} = (41)/(56) \pm 1.645 * \sqrt{((41)/(56) * (15)/(56))/(56)} \]`

Now, calculate the values:

`\[ \text{Confidence Interval} \approx 0.732 \pm 1.645 * 0.058 \]\[ \text{Confidence Interval} \approx (0.732 - 0.095, 0.732 + 0.095) \]\[ \text{Confidence Interval} \approx (0.637, 0.827) \]`

Therefore, the 90% confidence interval for the population proportion p is approximately (0.637, 0.827).