The solutions to the quadratic equation
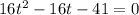 are
are
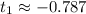 and
and
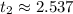 .
.
To solve the quadratic equation
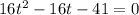 , we can use the quadratic formula:
, we can use the quadratic formula:
![\[ t = (-b \pm √(b^2 - 4ac))/(2a) \]](https://img.qammunity.org/2024/formulas/physics/college/2s78zm5vivjpknewmf6siqsr07jh69h2y2.png)
Here, a = 16, b = -16, and c = -41. Plugging these values into the formula:
![\[ t = (-(-16) \pm √((-16)^2 - 4(16)(-41)))/(2(16)) \]](https://img.qammunity.org/2024/formulas/mathematics/college/8zn3jnbzsnbhk6e53nqcycw5uertt6dgrh.png)
Simplifying further:
![\[ t = (16 \pm √(256 + 2624))/(32) \]\[ t = (16 \pm √(2880))/(32) \]\[ t = (16 \pm 8√(10))/(32) \]\[ t = (1 \pm √(10))/(4) \]](https://img.qammunity.org/2024/formulas/mathematics/college/3szx6szadnfw1axozssp0q6z9t1gnj6j7s.png)
So, the two solutions are:
![\[ t_1 = (1 - √(10))/(4) \approx -0.787 \]\[ t_2 = (1 + √(10))/(4) \approx 2.537 \]](https://img.qammunity.org/2024/formulas/mathematics/college/wxpkc52726mo168i9ct8gwl2q6w2z4x5v1.png)
These are the simplified radical forms of the solutions.