Question

a food truck did a daily survey of customers to find their food preferences the data is partially entered in the frequen ch table complete the table to analyze and answer the questions

Answer 1

Approximately 38.93% of respondents liked hamburgers but not burritos. The marginal relative frequency for customers who liked hamburgers is around 54.92%. "Does not like burritos" has the lowest joint relative frequency at approximately 13.52%.

Part A: Percentage of survey respondents who liked hamburgers but do not like burritos

To find the percentage of survey respondents who liked hamburgers but do not like burritos:

`\[ \text{Frequency of hamburgers and not burritos} = 95 \]`

`\[ \text{Total number of respondents} = 244 \]`

Percentage calculation:

`\[ \text{Percentage} = \frac{\text{Frequency of hamburgers and not burritos}}{\text{Total number of respondents}} * 100 \]`

`\[ \text{Percentage} = (95)/(244) * 100 \approx 38.93\% \]`

Therefore, approximately 38.93% of the survey respondents liked hamburgers but did not like burritos.

Part B: Marginal relative frequency of all customers who like hamburgers

To find the marginal relative frequency of customers who like hamburgers:

`\[ \text{Frequency of respondents who like hamburgers} = 134 \]`

`\[ \text{Total number of respondents} = 244 \]`

Marginal relative frequency calculation:

`\[ \text{Marginal Relative Frequency} = \frac{\text{Frequency of respondents who like hamburgers}}{\text{Total number of respondents}} \]`

`\[ \text{Marginal Relative Frequency} = (134)/(244) \approx 0.5492 \]`

The marginal relative frequency of all customers who like hamburgers is approximately 0.5492 or 54.92%.

part C: Category with the lowest joint relative frequency

To determine the category with the lowest joint relative frequency, calculate the joint relative frequencies for each category and identify the lowest value.

Joint relative frequency for "Likes burritos":
`\( (39)/(244) \)`

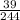
Joint relative frequency for "Does not like burritos" :
`\( (33)/(244) \)`

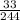
Joint relative frequency for "Likes hamburgers":
`\( (95)/(244) \)`

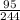
Joint relative frequency for "Does not like hamburgers" :
`\( (77)/(244) \)`

Among these, the category with the lowest joint relative frequency is "Does not like burritos" with a joint relative frequency of approximately 0.1352 or 13.52%.

Therefore, the category "Does not like burritos" has the lowest joint relative frequency.

A food truck did a daily survey of customers to find their food preferences. The data is partially entered in the frequency table. Complete the table to analyze the data and answer the questions: (PICTURE OF DATA DOWN BELOW) Part A: What percentage of the survey respondents liked hamburgers but do not like burritos? Show all work. (3 points) Part B: What is the marginal relative frequency of all customers who like hamburgers? Show all work (3 points) Part C: Which category has the lowest joint relative frequency?