Question

5. Graph the solution set of the system of inequalities. Which ordered pair is included in the solution set? OA. (0, -3) OB. (-5,-4) O C. (7,2) O D. (2,-6) y< x-3 y≤ − ²x+4 1 point​

Answer 1

The solution set, graphed from
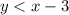`\(y < x - 3\)` and
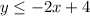`\(y \leq -2x + 4\)`, shows the region below both lines. Only (0, -3) falls within this area, satisfying both inequalities correct answer is a.

Let's solve the system of inequalities step by step to find the solution set.

Given inequalities:

1.
`\(y < x - 3\)`

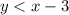
2.
`\(y \leq -2x + 4\)`

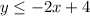
To find the solution set, we can start by graphing each inequality on the coordinate plane.

Graphing the inequality
`\(y < x - 3\):`

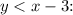
To graph
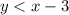`\(y < x - 3\)` , we'll draw a dashed line for
`\(y = x - 3\)` because it's a "less than" inequality. The region below this dashed line will represent the solution set.

Graphing the inequality
`\(y \leq -2x + 4\):`

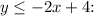
For
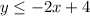`\(y \leq -2x + 4\)` , we'll draw a solid line for
`\(y = -2x + 4\)` since it's a "less than or equal to" inequality. The region below or on this line will represent the solution set.

From the graph, we can observe the shaded region that satisfies both inequalities.

Analyzing the Ordered Pairs:

Now, let's check which of the given ordered pairs is included in the shaded region:

A. (0, -3): This point lies within the shaded region.

B. (-5, -4): This point is outside the shaded region.

C. (7, 2): This point is outside the shaded region.

D. (2, -6): This point is outside the shaded region.

Therefore, from the solutions provided, the ordered pair that lies within the shaded region representing the solution set is A. (0, -3).