The equation x² + 8x - 12 = 0 has solutions:
 and
and
 found using the quadratic formula.
found using the quadratic formula.
1. Using the quadratic formula:
The quadratic formula is a general formula for solving quadratic equations. It states that the solutions of an equation of the form ax² + bx + c = 0 are given by:
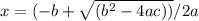
In this case, a = 1, b = 8, and c = -12. Plugging these values into the formula, we get:
x = (-8 ±

x = (-8 ±
 ) / 2
) / 2
x = (-8 ± 4
 ) / 2
) / 2
Therefore, the solutions are:
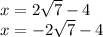
2. Factoring the expression:
This equation can also be solved by factoring the expression. However, in this case, factoring the expression is not as straightforward as using the quadratic formula.
Therefore, using the quadratic formula is the most efficient and general approach to solve this equation.
Complete question below:
what is a different form of the given equation
 ?
?