Answer:
Approximately
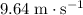 (assuming that the velocity of the exhaust is
(assuming that the velocity of the exhaust is
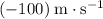 .
.
Step-by-step explanation:
When an object of mass
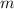 travels at a velocity of
travels at a velocity of
 , the momentum
, the momentum
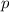 of this object will be
of this object will be
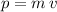 .
.
Assume that there is no external force on this spaceship. The total momentum of the ship and the exhaust will be conserved. In other words,
 .
.
Rearrange to find the momentum of the spaceship after releasing the exhaust:
 .
.
It is given that the spaceship and the exhaust were initial stationary. Hence, initial momentum will be
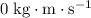 for both the ship and the exhaust.
for both the ship and the exhaust.
 .
.
Since the exhaust is of mass
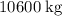 and velocity
and velocity
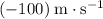 , the momentum of the exhaust after release will be:
, the momentum of the exhaust after release will be:
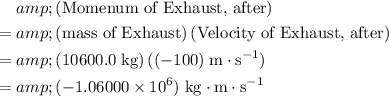 .
.
Divide the momentum of the spaceship by mass to find velocity:
 .
.