Question

A spaceship of mass spaceship = 110000.0 kg starts at rest (vi= 0), then accelerates by releasing

exhaust gas of mass gas = 10600.0 kg with a velocity of gas = -100. What is the speed of the spaceship

Answer 1

Approximately
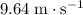`9.64\; {\rm m\cdot s^(-1)}` (assuming that the velocity of the exhaust is
`(-100)\; {\rm m\cdot s^(-1)}`.

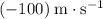Step-by-step explanation:

When an object of mass
`m` travels at a velocity of
`v`, the momentum
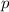`p` of this object will be
`p = m\, v`.

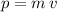Assume that there is no external force on this spaceship. The total momentum of the ship and the exhaust will be conserved. In other words,

`\begin{aligned}& (\text{Momenum of Spaceship, before}) \\ &+ (\text{Momentum of Exhaust, before}) \\ =\; & (\text{Momenum of Spaceship, after}) \\ &+ (\text{Momentum of Exhaust, after})\end{aligned}`.

Rearrange to find the momentum of the spaceship after releasing the exhaust:

`\begin{aligned} & (\text{Momenum of Spaceship, after}) \\ =\; & (\text{Momenum of Spaceship, before}) \\ &+ (\text{Momentum of Exhaust, before}) \\ &- (\text{Momentum of Exhaust, after})\end{aligned}`.

It is given that the spaceship and the exhaust were initial stationary. Hence, initial momentum will be
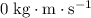`0\; {\rm kg \cdot m\cdot s^(-1)}` for both the ship and the exhaust.

`\begin{aligned} & (\text{Momenum of Spaceship, after}) \\ =\; & (0\; {\rm kg \cdot m\cdot s^(-1)}) \\ &+ (0\; {\rm kg \cdot m\cdot s^(-1)}) \\ &- (\text{Momentum of Exhaust, after})\end{aligned}`.

Since the exhaust is of mass
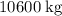`10600\; {\rm kg}` and velocity
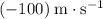`(-100)\; {\rm m\cdot s^(-1)}`, the momentum of the exhaust after release will be:

`\begin{aligned} & (\text{Momenum of Exhaust, after}) \\ =\; & (\text{mass of Exhaust})\, (\text{Velocity of Exhaust, after}) \\ =\; & (10600.0\; {\rm kg})\, ((-100)\;{\rm m \cdot s^(-1)}) \\ =\; & (-1.06000* 10^(6))\; {\rm kg \cdot m\cdot s^(-1)}\end{aligned}`.

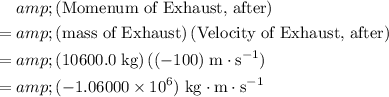Divide the momentum of the spaceship by mass to find velocity:

`\begin{aligned} & (\text{Velocity of Spaceship, after}) \\ =\; & \frac{(\text{Momentum of Spaceship})}{(\text{mass of Spaceship})} \\ =\; & \frac{((-1.06000* 10^(6))\; {\rm kg \cdot m\cdot s^(-1)})}{(110000.0\; {\rm kg})} \\ \approx\; & 9.64\; {\rm m\cdot s^(-1)}\end{aligned}`.